Dedução do Conceito de Integral Definida

     O que tem a ver a diferença de primitivas com a área localizada embaixo do gráfico de uma função?

     Para responder a essa pergunta precisamos fazer como que uma "engenharia reversa do Cálculo", ou seja, vamos demonstrar que a derivada da integral de uma função f(x) qualquer, num intervalo [a, x] é exatamente igual a essa mesma função f(x).

     Primeiramente representaremos a integral de f(x) no intervalo de [a, x] por "F" maiúsculo de "x":

"F" maiúsculo de "x" será chamado de primitiva de f(x)

     Depois aplicaremos a definição de derivada. Essa definição diz que a derivada de uma função é a razão incremental (x +  Δx) em um dado intervalo (Δx) quando este tende à zero:

Onde Δx tende à zero e é o incremento da função lnx.

     Sendo, então podemos substituir isso na definição de derivada e também dizer que "F(x + ∆x)" é a integral da função no intervalo de "a" até "∆x":

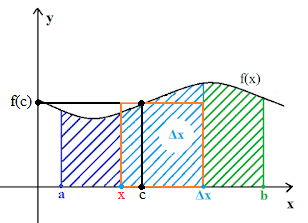
     Com base no gráfico abaixo, podemos observar que a integral de "a" até "Δx" menos a integral de "a" até "x" resulta na integral de "x" até "Δx":

 

     Substituindo temos:

     No século XVIII, Joseph Louis Lagrange, elaborou o Teorema do Valor Médio onde afirmava que em um dado intervalo da função, existe um ponto "c" cujo o "f de c", multiplicado pelo tamanho do intervalo, forma uma retângulo (o retângulo laranja da figura abaixo) que é exatamente igual a área embaixo do gráfico da função. O ponto "c" médio não é a metade do intervalo [x,  Δx]; o ponto "c" pode se movimentar convenientemente para esquerda ou para a direita até achar um f(c) que corresponda a altura de um retângulo equivalente à área embaixo do gráfico da função:

     Portanto, podemos substituirpor esse  triângulo de altura f(c) e base Δx:

     Cancelando Δx com Δx, ficamos com: 

     Em relação a esse limite, quando o Δx tende a zero, ele se reduz a "x", arrastando todos os pontos da função com ele:

     E portanto, quando Δx tende à zero,  "c" se reduz a "x" e também f(c) se reduz a f(x):

     Podemos confirmar isso aplicando o chamado "Teorema do Confronto" que diz que se os limites laterais do ponto "c" são iguais (nese caso, os limites laterais do ponto "c" tendem à x), então o valor de "c" é exatamente o resultado (idêntico) desses limites. Veja:

Pois "x" não depende de "Δx"

                                            

                                      

     Assim demonstramos que a derivada da primitiva de f(x) é igual a própria função f(x):

     Para finalizar, a partir de, vamos calcular a área embaixo do gráfico da função f(x) no intervalo [a,b]:

     Se inserirmos o "a" no lugar do "x", obteremos zero porque estaremos calculando uma área que vai de "a" até "a":

     Se inserirmos o "b" no lugar do "x", ficaremos com a seguinte expressão:

     Considerando G(x) e F(x) como sendo duas primitivas de f(x), temos que as derivadas dessa primitivas é igual a f(x):

     Sabemos, por definição, que duas primitivas diferem apenas por uma constante:, e podemos provar isso derivando essa expressão: 

     Levando em conta:

e

     Vamos calcular as expressões:

     Como , temos que:

     E substituindo na expressão , obtemos:

     Como "k" vale G(a), ficamos com:

     E fazendo os devidos ajustes:

     Assim, demonstramos algebricamente que, para calcular a área embaixo do gráfico de uma função, precisamos da diferença de uma Primitiva dessa função calculada no extremo direito do intervalo menos essa mesma Primitiva calculada no extremo esquerdo.

     Grande parte desse raciocínio que descrevi foi extraído dos seguintes vídeos: